시리니 님의 글을 읽고 필 받아서 확인했습니다. 무슨 글이냐고요? 입력된 수가 소수인지 아닌지를 판별하는 알고리즘에 관한 글이었습니다. 시리니 님의 글에 의하면,
- 입력한 수 n 이 n 이외의 정수로 나눠서 떨어지면 그 수는 소수가 아닙니다.
- 수학자들의 증명에 의해, n 대신에 root n 부터 위 1의 과정을 거쳐도 결과는 동일합니다.
- 루프를 돌면서 어떤 수에 나눠떨어지면 루프를 탈출해 소수가 아님을 알 수 있습니다.
이런 규칙에 의해 소수인지 아닌지를 알 수 있다고 합니다. 1번과 3번은 제 글에 쓰인 알고리즘과 동일하죠. 그런데 2번이 유독 눈에 띄더군요. 생각도 못한 사실입니다. root 값이라뇨? 와우! 대단합니다.
그래서 두 알고리즘의 연산 속도를 비교했습니다. time(NULL) 함수를 이용하였습니다. 아래는 이번 비교에 쓰인 코드입니다.
#include <stdio.h>
#include <math.h>
#include <time.h>
int CheckByDiv(unsigned int);
int CheckByRoot(unsigned int);
int main(void)
{
unsigned int number = 1;
long firstTime = 0;
long secondTime = 0;
printf("양의 정수를 입력하면 소수인지 알려줄게. : ");
scanf("%d", &number);
printf("\n");
firstTime = time(NULL);
if(CheckByDiv(number)) printf("이 수는 소수입니다. \n");
else printf("이 수는 소수가 아닙니다. \n");
secondTime = time(NULL);
printf("CheckByDiv() 함수에 의해 걸린 시간은 %ld초입니다. \n\n", secondTime - firstTime);
firstTime = time(NULL);
if(CheckByRoot(number)) printf("이 수는 소수입니다. \n");
else printf("이 수는 소수가 아닙니다. \n");
secondTime = time(NULL);
printf("CheckByRoot() 함수에 의해 걸린 시간은 %ld초입니다. \n", secondTime - firstTime);
return 0;
}
int CheckByDiv(unsigned int num)
{
register unsigned int div;
int value = 0;
for(div = 2; num % div; div++);
if(div == num) value = 1;
else value = 0;
return value;
}
int CheckByRoot(unsigned int num)
{
unsigned rootNum = (unsigned) sqrt(num);
register unsigned div = 0;
int value = 0;
for(div = rootNum; num % div; div--);
if(div == 1) value = 1;
else value = 0;
return value;
}CheckByDiv() 함수가 제 글의 알고리즘입니다. 일반적으로 쓰이는 거죠. 그리고 CheckByRoot() 함수가 시리니 님의 글에 소개된 알고리즘입니다. 두 함수의 차이는 sqrt() 함수로 rootNum을 이용하는가 아닌가입니다. 단 한 줄 차이입니다. 이 한 줄이 어느 정도의 차이를 보여줄까요?
아, 그리고 변수 div를 register로 선언하였습니다. 이것은 값을 메모리가 아닌 레지스터에 저장하라는 키워드입니다. 메모리보다 레지스터가 속도가 더 빠르다는 건 아시죠? 보통 반복문의 첨자로 쓰이며, 연산 속도의 향상에 도움이 됩니다. 두 함수 모두 div를 반복문의 첨자로 쓰이기 때문에 register로 선언한 것입니다.
그럼, 이제 결과를 보겠습니다.
에? 저거 정말인가요? 예, 정말입니다. CheckByRoot() 함수를 이용했을 경우 1초도 안 걸렸으므로 단순 배수 비교도 힘들게 되었습니다. 워메...
root 값을 이용하면 연산속도에서 큰 향상을 보일 수 있다는 걸 확인했습니다. 공돌이도 수학을 잘 해야 살아 남습니다. 응?
참고 문헌
알고리즘 :: 입력된 수가 소수인지 확인하자. :: http://hisjournal.net/blog/122
[뻘쭘한 알고리즘] 나는 네가 소수인지 아닌지 알 수 있다 (1) :: http://sirini.net/blog/737
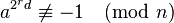for all 